Is Any Money Good Money? The Effects of IMF Credit on GDP Per Capita

I. Introduction

The International Monetary Fund (IMF) is a post-world war institution established in 1944 with a

mission to promote international financial stability and help ensure the mitigation of conflicts

caused by economic hardships. Since its founding, the IMF has evolved into a type of ‘lender of

last resort’ to its 190 member countries. With nearly $1 trillion in loan capacity and many types

of loan options,[1] many developing countries depend on the IMF for loans to help fund crisis

relief efforts or consolidate and payoff outstanding sovereign debts owed to other banks,

institutions, or governments.

The structure and terms of these IMF loans can vary depending on the borrower’s financial

health and severity of their debt accumulated from other sources. However, due to the nature of

the IMF mandate to alleviate international financial problem spots, the borrowers who come to

the IMF’s door are typically vulnerable and have been denied funds from most other credit granting

entities. The results of this phenomenon are that IMF loan conditions are known to be

very strict and controlling over the borrower, especially when it comes to certain developing

nations and regions such as South America, Africa, and the Caribbean that are especially prone to

financial insecurity as a legacy of colonization and lack of healthy government regimes.

The IMF holds the power to enforce policy decisions over its borrowers and has been known to

manipulate common tools such as interest rates and net exports in attempts to promote the

probability of loan repayment. These enforced changes can cause drastic shifts in monetary and

public policy doctrines, which then open opportunities for perceived negative changes in the

daily lives of a borrowing nation’s population. From obvious changes such as rising interest rates

causing hardships for a citizenry to obtain personal and private business loans, to far more

complex changes such as a mandatory decrease in net exports changing the types and sources of

food consumed in a county, IMF loan officers run the risk of enforcing ‘off-the-shelf’ conditions

that are neither tailored for a nation’s social landscape or healthy for their long-term growth.

These risks have raised concerns from scholars and advocacy groups that point out case studies

and trends that suggest IMF lending may be causing more detriment than intended on the path

towards debt repayment.

To empirically explore the nature of IMF lending and gain a simplistic analysis of whether the

outcomes of these loans are as beneficial as they are intended to be, panel data from the World

Bank will be utilized to find relationships between nations’ per capita GDP and use of IMF

credit. By merging data on these variables along with controls for inflation, population, and

measures of government health; it is possible to analyze this question using pooled OLS, fixed

effects panel, and random effects panel estimators. After applying controls and robustness

checks, pooled OLS regression results will show that use of IMF credit exhibits statistically

significant and positive effect on GDP per capita when taking into consideration all nations who

use IMF lending. Random effects and fixed effects regression modeling show a statistically

significant negative effect. Comments will be made regarding the validity and conclusions of

both methodological approaches.

II. The Data

The World Bank is an international investment bank that keeps detailed macroeconomic data on

all its 189 member nations, and whose work is complementary to that of the IMF. This is no

coincidence, as both organizations were founded during the post-war era with the shared goal of

promoting peace and stability worldwide. The World Bank focuses on connecting nations with

the investment tools they need for long-term economic growth and sustainability, while the IMF

actions are targeted more towards short-term monetary smoothing in the form of stabilizing

exchange rates and solving sovereign debt problems. The World Bank’s data it collects to aid in

these processes is compiled into one of the largest publicly available datasets on global

macroeconomic trends.[2]

This analysis will pull seven primary variables from this dataset and merge them together by

matching country and year and deleting all observations from aggregate measures to form a

panel dataset measuring the following:

GDP per Capita – Numerical variable that measures nation’s total Gross Domestic Product

divided by midyear population. Measured in USD.

Use of IMF Credit – Numerical variable measuring the aggregated amount of outstanding loans

issued to the nation by the International Monetary Fund. Measured in millions of USD.

Inflation – This variable is expressed as a number in percent form showing the increase in prices

calculated by using the CPI method of comparing a consumer basket to the set base year in each

nation.

Population – This variable simply measures the total population of a nation (including all ages

and genders) in millions collected by national level census estimates.

Corruption Control – Captures perception of to what extent public power is used for private

gain. It is also measured as a numerical variable between -2.5 and 2.5 representing standard

deviations away from the world mean. High number represents low corruption and vice versa.

Collected by aggregating survey data across many sources compiled by the Brookings Institute.

Government Effectiveness – This variable captures public perception of quality of government

services and policy implementation. It is a numerical output between -2.5 and 2.5 representing

standard deviations away from the world mean. Higher numbers represent positive government

perception and vice versa. Collected by aggregating survey data across many sources compiled

by the Brookings Institute.

Gini Index – Numerical variable ranging 0-100 that captures a nation’s level of income

inequality. Zero represents perfect equality and 100 represents perfect inequality. Calculated

using the Corrado Gini formula.

The number of observations varies greatly across variables, as measures such as Gini Index,

Corruption Control, and Government Effectiveness are not taken on a yearly basis or in a

methodological manner. Other variables such as GDP Per Capita, Population, and Inflation are

taken on a regular basis and are easily collected and verified. Table 1 shows a detailed

breakdown of each variable’s number of observations summary statistics. Gini Index has the

lowest number of observations at only two thousand, but the importance of this measure along

with its high rate of observation overlap with the other variables makes it justifiable to remain

included in the analysis.

Table 1 goes on to show the average GDP Per Capita is $9,241, the average population is 25

million, and the average usage of accumulated IMF credit is $705 million. Corruption Control

and Government Effectiveness have observed averages close to zero, which is expected as they

measure standard deviations. Variables such as inflation, Use of IMF Credit and GDP Per Capita

take on expansive ranges, while the measurements of government health are much more limited

in scope. Many variables include negative and zero values which make logarithmic

transformations unfeasible for much of the analysis.

III. Preliminary Analysis

To begin the analysis process, simple correlations will be ran before conducting several

variations of OLS regression modeling followed by hypothesis testing in order to parse out initial

findings and areas of significance.

Table 2 shows initial correlations between the variables. The strongest relationship is found

between the two Brookings Institute measures of government health: Corruption Control and

Government Effectiveness. However, with a correlation of 0.714, it is not a necessarily strong

correlation and does not raise concerns of multicollinearity or reveal any meaningful

relationships when analyzing the primary question. No other two variables show correlations

greater than 0.5 in absolute value. Perhaps most importantly, the correlation between GDP Per

Capita and IMF Credit is 0.193, which leaves no substantial claims able to be made off

correlation alone.

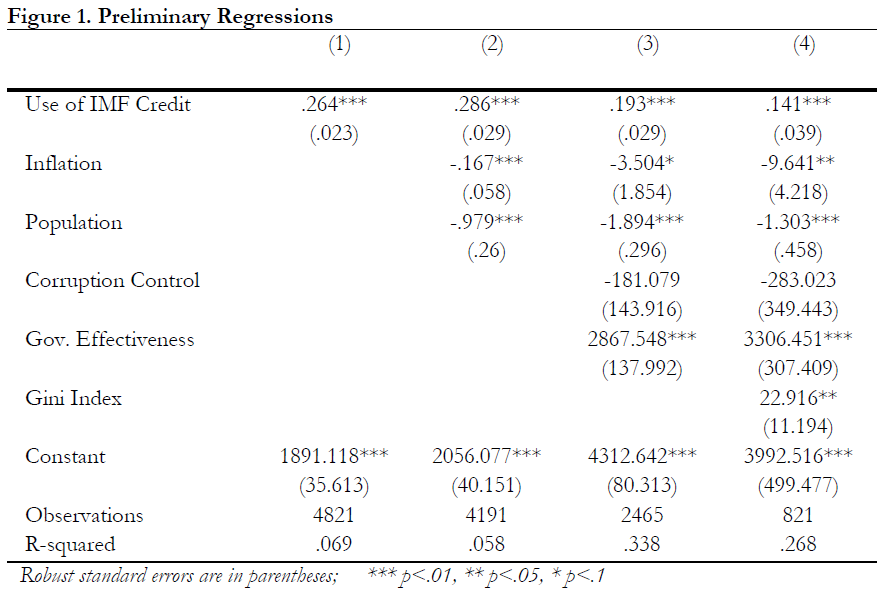
Figure 1 shows the initial regression models with the top four iterations displayed. The first

included regression iteration includes only the amount of IMF credit used. This result

immediately shows IMF credit having a positive and statistically significant impact on GDP per

capita, with an interpretable magnitude of a $0.26 average increase in GDP per capita with every

$1 million increase in IMF credit. When common macro measures are included as controls in

iteration two, the same result for IMF credit hold, while also boosting magnitude to a $0.286

increase in GDP per capita for each $1 million in credit. Both controls of inflation and population

also come out significant at the 0.01 level, however their impact on GDP per capita is negative. A

$0.167 decrease is observed with each additional percent increase in prices, and a $0.979

decrease results from each million person increase in population on average.

Iteration three adds the effects of Brooking’s government health measures. The impact of

corruption control is not statistically distinguishable from zero, while the effect of government

effectiveness is significant and positive with each standard deviation increase in quality of

government services resulting in a $2,867 increase in GDP per capita on average. This result is

immense compared to all other magnitudes observed so far. This is likely due to the small range

of possible outcomes, the large jump in value a standard deviation measures, and the fact that

wealthy countries are typically able to offer the highest quality of government services. Other

important observations are that inflation loses its significance, IMF credit loses $0.09 of

magnitude, and that the model’s R-squared is drastically higher with the inclusion of the two new

variables.

The fourth and final iteration introduces the Gini Index measure. The Gini measure comes out

significant and positive at the 0.05 level, which an interpretation of a $22 average increase in

GDP per capita with every increase unit increase in the 1-100 measure. This suggests that GDP

per capita is positively related with income inequality within our model. This iteration was

purposefully designed to determine the optimal model for advanced analysis, as the limited

observations of the Gini Index needed to be weighed against the benefits of its inclusion.

The Gini Index shrunk the effect of IMF credit down to a magnitude of $0.14 while also

returning significance to the effect of inflation and being significant itself. The number of

observations drop as expected to 821 from 2400 while the R-squared measure also drops by 0.07.

However, vif scores do not suggest that any multicollinearity is introduced with the inclusion of

Gini Index, and the importance of adding additional controls in the already limited model takes

precedent in this situation. Furthermore, the joint hypothesis test including all three variables

proved to be statistically significant. Although a hard decision to make, iteration four and the

Gini Index is chosen as the optimal model to continue to advanced analysis.

It should be noted that robust standard errors were used within all initial regression modeling, as

concerns of heteroskedasticity were present in all model specifications. The White test was

conducted to each of the four model interactions, and it was found that heteroskedasticity was

present in all four. Therefore, robust standard errors were turned to in order to dampen any

negative effects of the heteroskedasticity and to obtain more appropriate and trustworthy

coefficient estimates.

The potential issues caused by omitted variable bias also raise concern in this context, however,

much less can be done to address this. Given the nature of the primary research question and how

intricate the factors at play are, there is a large chance that multiple explanatory variables are

endogenous as a result of unobserved factors that the dataset does not have information on. This

could cause the estimators to be biased but given the relatively limited amount of data this

project has access to, there are no obvious avenues to avoid this issue. This is another

justification for including the Gini Index variable in the final iteration, as its inclusion will

hopefully control for even more unrealized variables that are playing a part behind the curtain of

this research question.

While the results of these initial estimators provide interesting and helpful results to begin

expanding upon further, in and of themselves, they leave much to be desired. These estimates are

referred to as pooled OLS estimates and do not explicitly address the panel structure of our

dataset. They are not capturing any of the unique country-specific factors that are very much

alive within the observations. The pooled OLS estimator clumps all observations together and

creates a single slope and intercept based off the values every country takes on across time. We

know, however, that it is likely that county-specific differences would reveal themselves if slopes

were created within each clustering of a nation’s time observations and would not result in a

singular intercept. These are relationships that must be controlled for to derive the most accurate

and reliable results possible. These issues will be addressed in the part IV, as more advanced

panel estimators will be utilized to control for these factors.

IV. Advanced Analysis

Given that the dataset contains 190 contries all with their own unique GDP per capita trajectory

throughout time along with unique social, political, cultural, and socio-economic landscapes; a

panel estimator is necessary to consider when analyzing a question such as that of IMF credit

effects on GDP per capita. Both a random effects and fixed effects panel estimator will be run in

this analysis, however the case will be made for the superiority of the fixed effects estimator in

this situation. These results will then be compared to the pooled OLS estimator drawn from the

preliminary analysis revealing some very stark differences in both coefficient directions and

magnitudes.

The introduction of the random effects estimator undoubtably has potential to add further

efficiency to our estimates, as in theory it is able to account for individual country-level random

effects while the pooled OLS estimators from Figure 1 do not explicitly account for these pivotal

country level differences. The random effects (RE) estimator is the Feasible Generalized Least

Squares (FGLS) estimator for the country-level random effects by grouping the observations by

country. When its assumption hold, this makes the RE estimator more efficient than the pooled

OLS estimator, as it is able to derive a different intercept for each individual country grouping.

The pooled OLS estimator, on the other hand, was blind to these clusters and had to estimate a

slope and intercept based solely on the combined observations of every nation, hence the

‘pooled’ term used to describe it. The result is that the RE estimator can provide much more

precise estimates if the assumptions needed hold.

The gains in efficiency the RE estimator realizes from this difference are not without the

downside of more stringent assumptions having to be made. The RE estimator is built upon the

‘random effects assumption’ that assumes that the covariance of all unobserved individual

heterogeneity must be uncorrelated with all explanatory variables present in the model. It also

assumes strict exogeneity, meaning that the explanatory variables must be uncorrelated with the

present and future values of the error term. Both the random effects assumption and the

assumption of strict exogeneity are likely not valid in this data setting, as concerns of

endogeneity within the model were pointed out previously.

Without these assumptions holding, the RE estimator loses much of its power and becomes

inconsistent and biased. The pooled OLS estimator, on the other hand, relies only on

contemporaneous exogeneity and no random effects assumption, which requires only that the

explanatory variables be uncorrelated with the error term of the current time period. This is a

much weaker assumption to be violated, however, as stated before, the pooled OLS estimator

does not include controls for group level random effects as a result.

Furthermore, concerns of heteroskedasticity have also already been raised and accounted for as

best as possible within the pooled OLS estimator, which leaves the efficiency of the RE estimator

further into question even when compared to that of the pooled OLS. These issues create a

trickey environment, as the efficiency gained by grouping observations by individual country has

obvious benefits, but the strength of assumptions needed for the RE estimator to hold seems to

be too heavy for the dataset. Thankfully, the fixed effects (FE) panel estimator may provide a

helpful alternative.

The fixed effects estimator is extremely powerful in this situation, as it sidesteps the need for the

random effects assumption to hold. The FE estimator essentially takes all of the unobservable

country-level variables that are time constant and averages them out across time to control for

their effects. This process referred to as a ‘within transformation’ eliminates all individual time

constant heterogeneity from the error term and leaves an estimator that is immune to time

constant unobserved variables that cause bias and inconsistency issues to plague both the pooled

OLS and RE estimators. This element of the FE estimator makes it a prime candidate for this

specific data problem and provides an avenue to escape from the problems caused by these

previously broken assumptions.

Figure 2 shows the pooled OLS estimator (1) along with both the RE estimator (2) and the FE

estimator (3) all running the same model used as the final iteration from Figure 1.